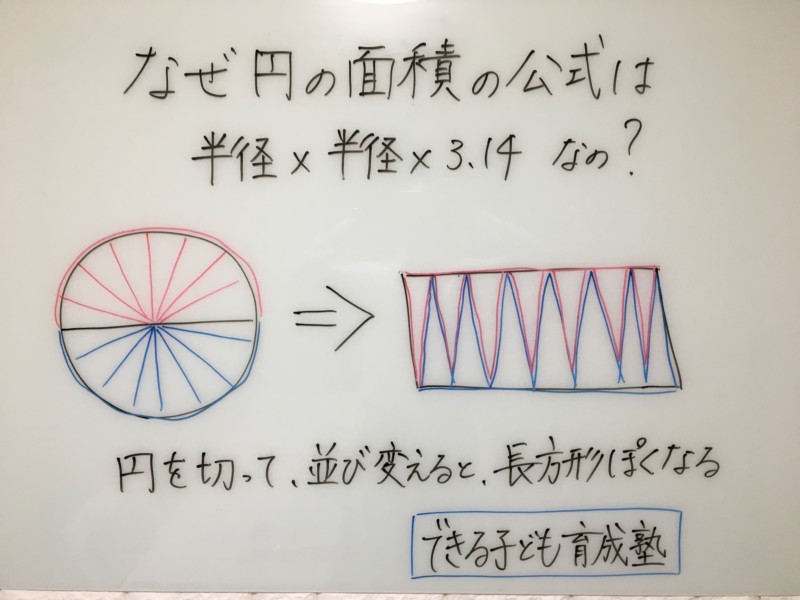
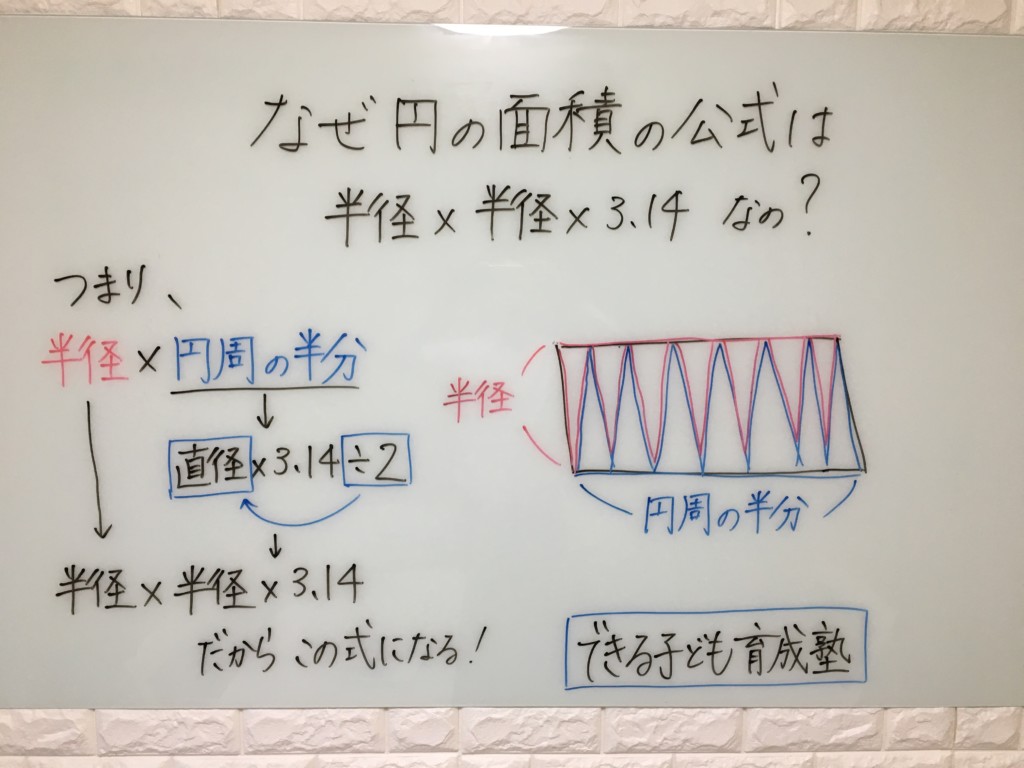
円の面積は、なぜ【半径×半径×３．１４】なのでしょうか？

決まりだから？

いえ、違います。

ちゃんと理由があるのです

円を細かく切って、並べ替える

円をピザのように細かく切ります。

その切ったピザのような形を、尖っている同士を向かい合わせて並べていきます。

すると、長方形のような形になります。

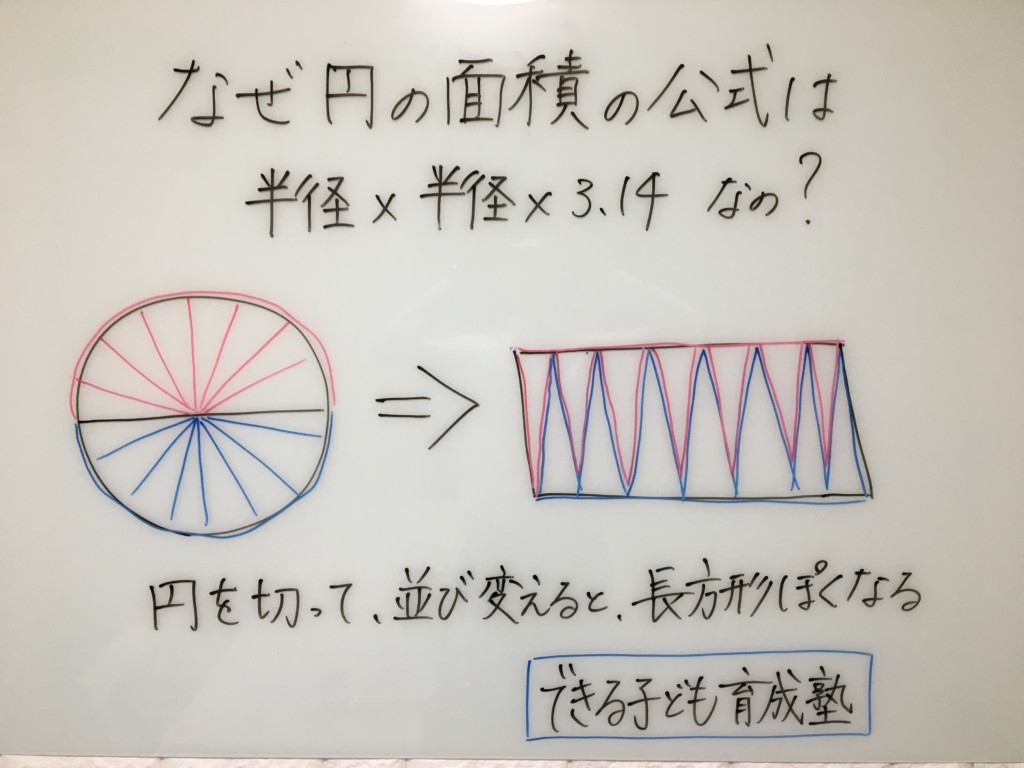
長方形の面積の求め方に合わせる

長方形の面積の求め方は、【縦×横】ですよね。

ピザのように切って、並び替えた図形の縦と横が円のどの部分になるか見ると、

縦・・・半径

横・・・円周の半分

つまり、【半径×円周の半分】になります。

【半径×円周の半分】をもっと細かくする

【半径×円周の半分】をもっと分解していきましょう。

半径・・・そのまま

円周の半分・・・直径×３．１４÷２

こうすると、【半径×直径×３．１４÷２】になります。

これをさらに分解すると、

半径・・・そのまま

直径×３．１４÷２・・・半径×３．１４（直径÷２を先に計算して、半径にした）

もとの式に当てはめると、

【半径×半径×３．１４】

円の面積を求める公式になりました！

【大人気】塾長のYouTubeチャンネル『慶太の学校』

この記事は「できる子ども育成塾」の塾長が書いています。
できる子ども育成塾は、江戸川区小岩にある元小学校教師が教える個別指導塾です。

入塾について、その他のご質問などは、下のお問合せフォームよりお送りください。
お電話でのお問い合わせをご希望の方は、こちらにご連絡ください。
080-7278-1025